Calculating and Using Percentages

A company that sells its products online wants to know how common it is for someone who visits their web site to end up buying something. Suppose they track their web traffic and sales for one month and find that 2,405 people buy a product online.

By itself, this number does not give a sense of how common it is for web site visitors to buy something, though. We would also need to know how many people actually visit the web site.

The number of sales is only meaningful when we compare it to the total number of visitors. The standard way to make this kind of comparison is to compute a percentage.

Course of Content:

• Finding a Percentage of a Number
• Percentage Change
• Percentage Increase and Decrease
• Percentage Difference
• Averages of Percentages

Finding a Percentage of a Number

When comparing two quantities, we usually distinguish between a target quantity and a base quantity. The target quantity is the one we are interested in measuring. In the example above, the target quantity is the number of visitors who make an online purchase, 2,405.

The base quantity is the quantity relative to which we measure the target. In our example, the base quantity is the total number of web site visitors.

Suppose 2,500 people visit the web site during the month. This would be the base quantity. We can state a target-to-base comparison as a rate, using a sentence like “2,405 out of 2,500 web site visitors made an online purchase.”

Now, given this rate, how many purchases should we expect when the web site gets 5,000 visitors? Since we have doubled the base quantity, we should also double the target quantity and therefore predict that 4,810 of the 5,000 visitors will make a purchase.

We can summarize this by saying that the rate 2,405 out of 2,500 is equivalent to the rate 4,810 out of 5,000. In general, two rates are equivalent to each other when you can multiply the target and base of one rate both by the same number and get the target and base of the other rate.

Example

Find two other rates equivalent to 2,405 out of 2,500.

Solution

While rates do give a sense of how big a target is relative to a base, it would be better to have a single number to measure relative size. This is where percentages come in.

A percentage is a rate in which the base has been scaled to equal 100. (The word “percent” comes from the Latin per centum, which means “by one hundred”.)

For example, consider the rate 75 out of 300. To find the percentage, we will need to find an equivalent rate for which the base is 100. If we multiply the original base 300 by 1/3, we get a new base of 100. We should therefore also multiply the original target by 1/3 to get the new target: 75 x 1/3 = 25.

We have shown that the rate 75 out of 300 is equivalent to 25 out of 100. The new target 25 is the percentage, and we can now say that 75 is 25 percent (in symbols, 25%) of 300.

Let’s look more closely at how we arrived at 25%. We first had to scale 300 down to 100.

This was done by multiplying 300 by 1/3 – notice that 1/3 is just 100 divided by the base 300. We then multiplied 1/3 by the target 75 to get the percentage. This leads us to the following formula for calculating percentages:

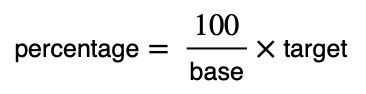
Rearranging the factors on the right side a little, we get the more familiar version of this formula:

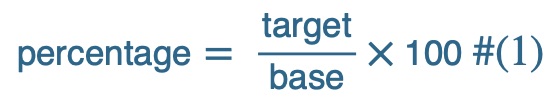
Example

Find the percentage of 2,405 out of 2,500.

Solution

According to Formula (1), we have that the percentage is

2,405 / 2,500 x 100 = 96.2%

You should check that the other equivalent rates we have seen (namely 4,810 out of 5,000; 7,215 out of 7,500; and 481 out of 500) all determine the same percentage.

The above example shows how to find a percentage when you are given the target and base quantities. What if, instead, you are given a base and a percentage, and you have to find the target? Suppose you want to find 40% of 280. The base is 280, and our job is to find the target. Using Formula (1), we can see that

target / 280 x 100 = 40

If we solve this equation for the target, we get

target = 280 x 40 / 100

This suggests the following formula for calculating a target when you are given a base and a percentage:

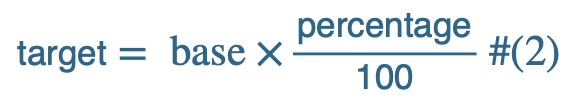
Example

Suppose you are selling your home, and your real estate agent’s commission will be 6% of your home’s sale price. If your home sells for $350,000, how much will the commission be?

Solution

We have to find 6% of 350,000. Using Formula (2), we have

350,000 x 6 / 100 = 21,000

The real estate agent’s commission will be $21,000.

In practice, Formula (2) is often used in conjunction with a small shortcut. When a number is divided by 100, the decimal point is moved two places to the left. For example, 65.3/100 = 0.653. When there is no decimal place, you can imagine one after the last whole number digit.

For example, 73/100 = 0.73. When dividing a number with a single whole number digit by 100, we must insert a placeholder zero. For example, 5.3/100 = 0.053.

Percentage Change 

The U.S. federal debt at the end of 2001 was $5.77 trillion and grew to $6.20 trillion by the end of 2002.  At the end of 2005 it was $7.91 trillion and grew to $8.45 trillion by the end of 2006. Which year saw a more significant increase in debt?

At first, this seems to be a very easy question to answer; we could simply compare the amounts by which the debt grew during the two periods, and we could immediately see that the debt increase was bigger from 2005 to 2006. 

However, we can argue that the change from 2001 to 2002 was actually more significant. Instead of considering only the increases in the debt amounts, let’s look at the debt increases relative to the initial debt amounts. We can measure these relative increases by computing percentage change.

The percentage change in a quantity is the percentage whose target is the change amount and whose base is the initial amount. (The absolute value in the formula below ensures that we can ignore any negative signs that show up in our calculation.)

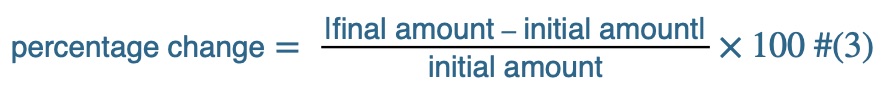
For 2001 to 2002, the percentage change in the federal debt was

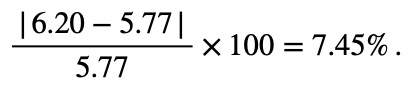
For 2005 to 2006, the percentage change was 

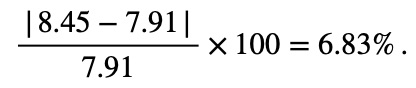
We can therefore say that the debt increased more significantly from 2001 to 2002 since the percentage change was bigger.

Example

A husband and wife are both trying to lose weight. The husband’s weight drops from 220 pounds to 197 pounds. The wife’s weight drops from 143 pounds to 125 pounds. Whose weight loss is more significant?

Solution

The husband lost 23 pounds, and the wife lost 18 pounds. However, to compare the significance of these changes, we should compute their percentage changes using Formula (3).

The percentage change for the husband is

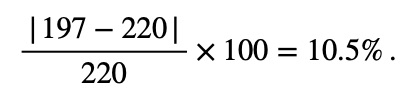
The percentage change for the wife is

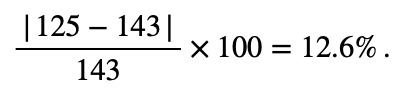
Since the wife’s percentage change is bigger than the husband’s, we can say that her weight loss amount is more significant.

Percentage Increase and Decrease

We often hear statements like, “We must increase productivity by 40%” or “You could lower your heating bill by 15%”. What does it mean to increase or decrease a quantity by a percentage?

Suppose your hourly wage is $25 and you are told you will be receiving an 8% raise. What will your new wage be? Your wage is increasing by 8% of $25, which, by Formula (2), is 25 x 0.08 = 2. Thus, your new wage will be $25 + $2 = $27.

We can streamline the calculation in the previous paragraph. The new wage was computed by finding the value of 25 + 25 x 0.08. We can rewrite this expression as 25 x 1 + 25 x 0.08 and then factor out the 25:  25 x (1 + 0.08). This simplifies to 25 x 1.08. This suggests the following method for increasing a quantity by a percentage.

To increase a quantity by a percentage, multiply the quantity by 1 + r, where r is the percentage converted to a decimal number (by moving the decimal point two places to the left).

Example

The enrollment at a university is 15,600 students and is projected to increase by 4% next year. What is the projected enrollment for next year?

Solution

1. We first must convert the percentage to a decimal by moving the decimal point two places to the left:  4% = 0.04.  
2. We then add this converted percentage to 1:  1 + 0.04 = 1.04.  
3. Finally, we multiply the given quantity by the result of the previous step:  15,600 x 1.04 = 16,224.

The projected enrollment for next year is 16,224 students.

Suppose now that we want to decrease a quantity by a percentage. For example, suppose you work 48 hours per week, but you are told to cut your hours by 15%. How many hours will you now be working?

We can proceed as above, with one small difference. We will start by calculating 15% of 48, which is 48 x 0.15 = 7.2. However, we then subtract this from the initial amount. So, your new number of hours will be 48 – 7.2 = 40.8.

As above, the previous calculation can be condensed. We decreased 48 by 15% by computing 48 – 48 x 0.15. We can write this as 48 x 1 – 48 x 0.15 and then factor out the 48, obtaining 48 x (1 – 0.15), which equals 48 x 0.85. This leads us to the following method for computing a percentage decrease.

To decrease a quantity by a percentage, multiply the quantity by 1 – r, where r is the percentage converted to a decimal number (by moving the decimal point to places to the left).

Example

A store advertises a going-out-of-business sale with everything 70% off. What will be the sale price of an item that was originally priced at $37.50?

Solution

1. First, convert the percentage to a decimal:  70% = 0.70.
2. Then subtract the converted percentage from 1:  1 – 0.70 = 0.30.
3. Finally, multiply the initial price by the result of the previous step:  37.50 x 0.30 = 11.25.

The sale price will be $11.25. 

Related: Percentage Increase Calculator

Percentage Difference

In all the examples of percentage changes in the last two sections, the quantity whose change we were measuring had initial and final values – an initial debt changes to a final debt, an initial weight changes to a final weight, etc. 

In each of these examples, the percentage change measured the change in the quantity relative to the initial amount of the quantity. What do we do when we want to compare two quantities for which there is no notion of “initial” and “final”? One way to do this is to compute the percentage difference.

Suppose on a given day, the temperature in Phoenix, Arizona, is 95°F and in Detroit, Michigan, is 68°F. Neither of these quantities is an initial or final temperature, so the percentage change is not a meaningful measurement of how much they differ. 

Instead of comparing the difference in temperatures to either of the given quantities, like you would for a percentage change, we could compare the difference to the average of the two temperatures, which is

95 + 68 / 2 = 81.5

The percentage difference between the two temperatures is then defined to be the percentage with the difference as the target and the average as the base:

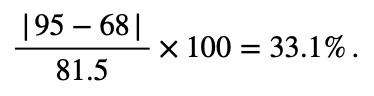
In general:

Example

Your mother’s height is 66 inches, and your father’s is 71 inches. Compute the percentage difference between these heights.

Solution

Since 66 and 71 are not initial and final amounts of a single variable, percentage difference is more appropriate than percentage change. To use Formula (4), we first need the average of the two heights:  (66 + 71)/2 = 68.5. The percentage difference is therefore

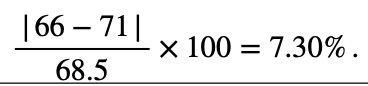
Averages of Percentages

Suppose a basketball player makes 45% of her 2-point shots and 35% of her 3-point shots. Can we conclude that she makes 40% of her shots overall? After all, 40 is the average of 35 and 45.

Not necessarily. It depends on how many of each shot was taken. Suppose she takes 360 2-pointers and 140 3-pointers. Since she made 45% of her 2-pointers, the total number of 2-pointers she made was 360 x 0.45 = 162. Likewise, the total number of 3-pointers she made was 140 x 0.35 = 49. 

That means she made a total of 162 + 49 = 211 shots, and she took a total of 360 + 140 = 500 shots. The percentage of shots she made was therefore

211 / 500 x 100 = 42.2%

We see that the overall percentage is not the average of the two individual percentages. Let’s trace back through the previous calculation to develop a formula for finding the average of two percentages.

The overall target, 211, in the percentage above is the sum of the two individual targets, 162 and 49. We found these targets using Formula (2):  162 = 360 x 0.45 and 49 = 140 x 0.35. So, the overall target equals 360 x 0.45 + 140 x 0.35.  

The overall base, 500, in the percentage above is the sum of the two individual bases, 360 and 140. We can therefore see that the overall percentage can be written as

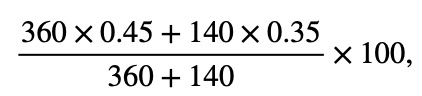
which can be simplified to

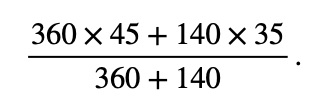
This leads us to a formula for the average of two percentages.

Suppose p1 is a percentage whose base is b1 and p2 is a percentage whose base is b2. The average of p1 and p2 is

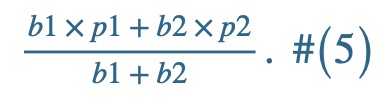
Example

In a math class, the homework assignments have a total of 600 possible points, and the exams have a total of 800 possible points. A student has earned 85% of the homework points and 72% of the exam points.What is his overall percentage of points earned?

Solution

Using Formula (5) with b1 = 600, p1 = 85, b2 = 800, and p2 = 72, we get that the student’s overall percentage is

Returning to the scenario posed in the opening paragraph, we can now see that the question about how common it is for web site visitors to make a purchase is best answered by computing a percentage. 

Percentages provide a standardized way to express the magnitude of a quantity relative to some other quantity, and they provide meaningful, immediately accessible metrics when discussing sizes, changes, and differences.